When Queues Explode
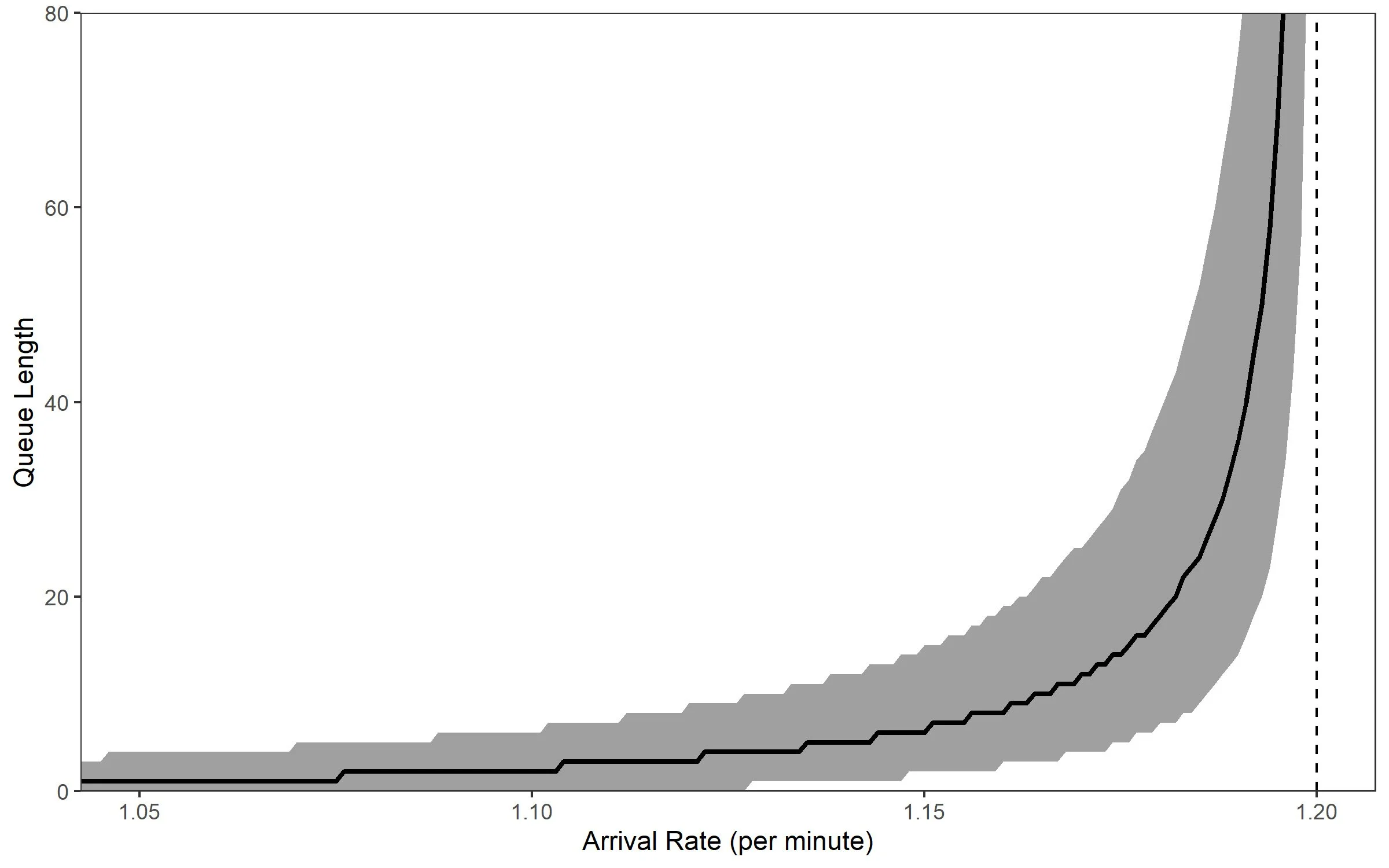
A somewhat unintuitive result is that if demand is random, as demand approaches delivery capacity, the queue size will tend to grow without bound. Say we are operating a fuel station, and can service 6 cars every 5 minutes (or 1.2 cars per minute). Car arrivals are random as we don't control our customers, and they will arrive at some rate, x cars per minute. Clearly if more than 6 cars arrive every 5 minutes (x > 1.2) the queue will grow to infinity as we cannot service the demand. But the queue can grow very large even with x at a serviceable level (x < 1.2). This is demonstrated in the plot below. It shows the median and interquartile range of the queue length as we increase the arrival rate, x.
Estimating this curve for complex systems is very difficult but thankfully there are two reasons we can avoid this exercise.
The first is that feedback will ensure this rarely happens in practice. If I see 60 cars at a service station, it doesn't matter how cheap the fuel is, I'll go elsewhere or come back at another time. Or consider the cases of truck arrivals at a distribution centre or ship arrivals at a port, the planners actually have control over the demand and their ordering behaviour. Of course this means that we now need to consider the feedback mechanism, which can also be complex, but much more useful!
The second reason applies even when there is no feedback mechanism. It is sufficient to know that high queue lengths are unacceptable. If we have enough precision to know that the queue length is too high, we don’t need to know how high exactly because we’re want to avoid it happening. We can then spend our time estimating the queue length for more reasonable situations. This idea doesn't work as well for such things as disaster or force majeure planning, but that's a topic for another day.
If you're wondering what is contributing to your queues, or hoping to reduce them, let's have a chat about how we can use advanced analytics to understand your logistic system (Hello@NorthCardinal.com.au).